Previous Topic

Next Topic

Book Contents

Book Index

Two-Tissue Compartment Model with Basis Functions

The 2-Tissue (BFM) model implements fitting a two-tissue compartment model in each image pixel. It is based on an analytic solution of the system of differential equations which results in the calculation of two eigenvalues a1 and a2.

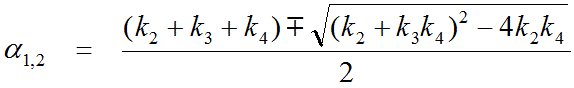
The expected tissue activity is obtained by the convolution of the input function with a sum of two decaying exponentials plus a contribution from whole blood.

This operational equation which can be fitted to the data has 5 parameters: q1, q2, a1, a2, vB . It is linear in the parameters q1, q2, vB, and nonlinear in a1, a2 . The q1 and q2 parameters are also a combination of the rate constants.

The basis function method by Hong and Fryer [43] performs the data fitting in the following way:

  1. For a certain tracer the physiological range of k2, k3, k4 can be determined. These values can be translated into a range of a1 and a2 values which can be expected in the data. With FDG, for instance, a1 Î[0.0005,0.015]min-1 and a2 Î[0.06,0.6]min-1.
  2. The functions e-a1 and e-a2 are called the basis functions. They are pre-calculated for tabulated a1 and a2 values which span the prescribed ranges.
  3. In fitting the data, each combination of a1 and a2 is examined: the input curve is convolved with the pre-calculated exponentials, and then the operational equation is fitted with respect to the remaining parameters q1, q2, vB. Since all of them enter linearly, the solution is unique and can be quickly calculated. For each of the calculations the chi-square criterion is recorded.
  4. Since the fitting has to be performed for each combination of a1 and a2, N2 results are obtained if N is the number of table entries. Finally the combination q1, q2, vB, a1, a2 with minimal chi square is considered as the solution.

In the case of irreversible binding k4 is assumed to be zero. Hereby the number of fitted parameters is reduced and the operational equation simplifies to

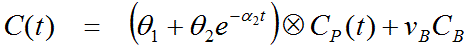
It is notable that in this case only one basis function appears in the equation. Therefore, the number of linear fits is reduce from N2 to N, making pixel-wise fitting very fast.