One-way ANOVA for 3 or 4 Groups

The one-way ANOVA compares the means between the groups and determines whether any of those means are significantly different from each other.

The NULL hypothesis (H₀) assumes that all group population means are equal. The alternative hypothesis (H_a) is that there are at least two group means that are significantly different from each other. If the result is statistically significant, the alternative hypothesis is accepted.

The one-way ANOVA is a statistic test can only detect that least two groups are different, but not which ones. To this end a post-hoc comparison test needs to be applied. The ANOVA script applies the Tukey's HSD (Honest Significant Difference) test.

Assumptions

The results of a one-way ANOVA can be considered reliable as long as the following assumptions are met:

• the response variable (the dependent variable) is normally distributed;
• the samples are independent;
• the variances of populations are equal.

ANOVA Configuration

The configuration window is illustrated below.

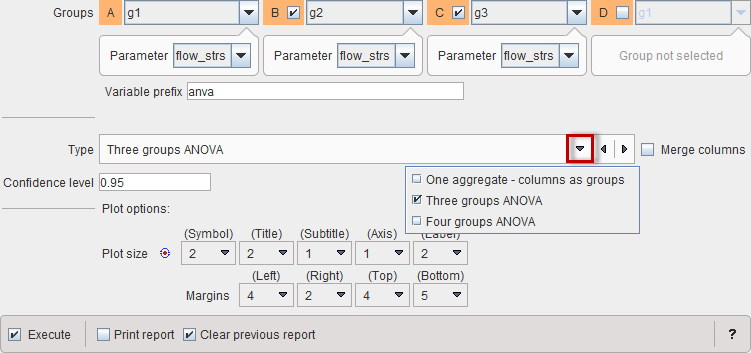
Basically, there are two usage types:

1. The groups to be compared are arranged as the columns in a single aggregate. This situation is reflected by the One aggregate - columns as groups selection as the analysis Type.
2. The groups to be compared are organized in separate aggregates. The script can handle 3 or four groups. If Merge columns is enabled, the data of all columns will be pooled, otherwise the ANOVA analysis is performed per column.

ANOVA Results

The script produces result tables related to the ANOVA (anva_result) and Tukey (anva_tukey) as well as plots for the results visualization.

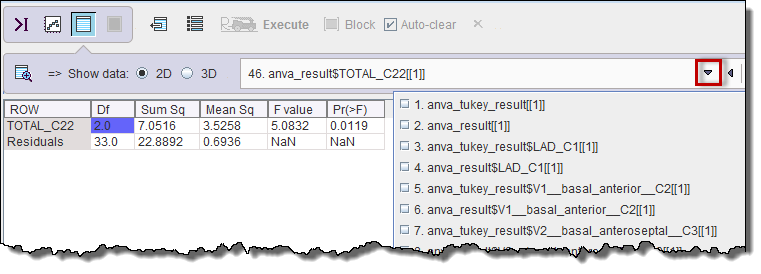
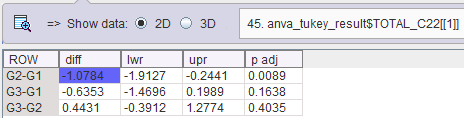
Note the p-value which is below 0.95, indicating that there is a significant difference which can be localized for G2-G1 in the Tukey table below. For r G2-G1 p<0.05 where it is >0.05 for the other comparisons.

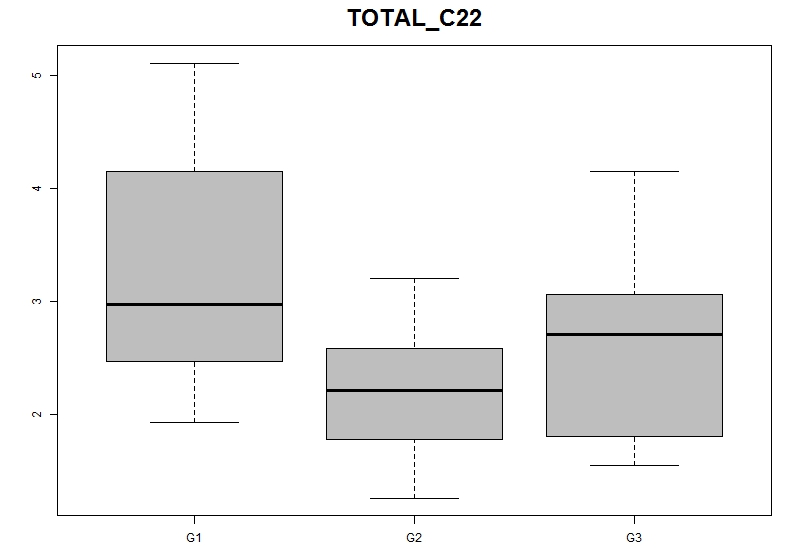
The plot layout contains a box plot per VOI, showing the characteristics of the groups next to each other. In the example below the difference between G1 and G2 is supported.

The second plot which is available per VOI visualizes the 95% confidence interval of the group differences.

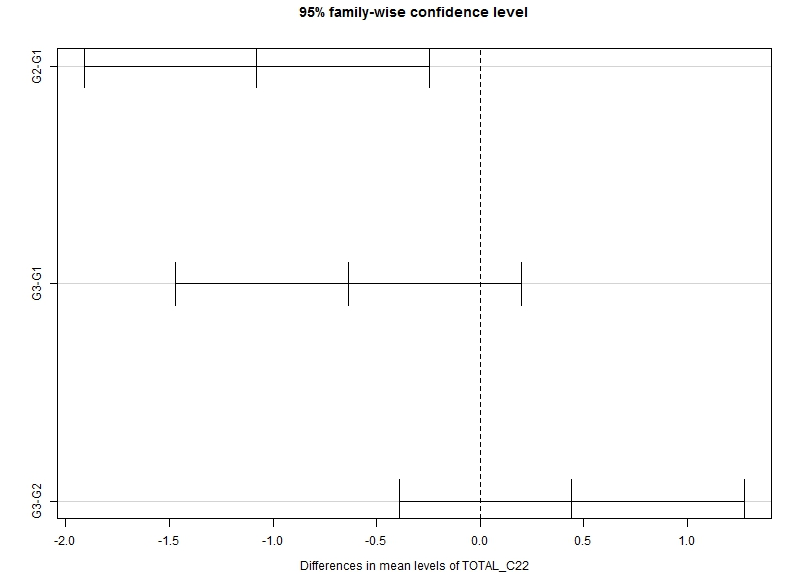
If zero is not included in the confidence interval, the difference is significant.